Introduction
Note: L’article original a été publié sur le blog de mon entreprise https://blog.sec-it.fr/.
La stéganographie est le procédé de dissimulation d’un message confidentiel au sein de données. Dans le cadre d’un cours enseigné à l’ESNA, j’ai proposé une série d’exercices et challenges stéganographiques dont voici les corrigés. Les challenges sont triés par difficulté croissante.
Challenges
PDF est un challenge proposant un fichier PDF. Ce dernier est une copie du PDF de présentation de L’ESNA, et possède un total de 2 pages.
En stéganographie, les fichiers PDF sont réputés leurs différentes interprétations selon les lecteurs, mais également pour la superposition des objets PDF rendant parfois invisibles certains objets comme des blocs de texte ou des images. Ces mêmes objets PDF peuvent être parfois renseignés dans la table de référence du fichier mais non affichés sur le document.
Pour ce challenge, il s’agissait d’un simple texte noir sur fond noir :

Peu de lecteurs PDF permettent la sélection d’un texte caché comme celui-ci, le lecteur proposé par Google Chrome propose toutefois de sélectionner l’ensemble du texte (CTRL+A). Il suffit ensuite de copier puis coller le contenu dans un fichier texte.
Nous nous retrouvons donc avec la chaine de caractère 92149279564403446967073413054727415165.
Il s’agit d’un entier codé sur la base 10.
Afin de convertir cet entier en chaine de caractère, il est possible de le convertir en binaire ou hexadecimal puis en texte, ou bien d’utiliser la commande python3 suivante :
import binascii
a = f"{92149279564403446967073413054727415165:0>4X}" # convertion en hexa
binascii.unhexlify(a) # ici a = "45534E417B737041414141414163657D"
# b'ESNA{spAAAAAAce}'
Une autre solution en ruby:
require 'ctf_party' # gem install ctf-party
'92149279564403446967073413054727415165'.dec2hex.hex2str # => 'ESNA{spAAAAAAce}'
Flag : ESNA{spAAAAAAce}
Music please
Pour ce challenge un fichier challenge.wav était fourni.
Le fichier wav dure 31 secondes et propose le début de la musique IMANU - Memento.
Les oreilles les plus affinées reconnaîtront un léger grésillement présent uniquement sur les 4 premières secondes du fichier.
Ce grésillement plutôt aigu devrait être visible dans les hautes fréquences du spectre audio du fichier wav.
Pour l’observer, il suffit d’ouvrir le fichier à l’aide de l’outil audacity.
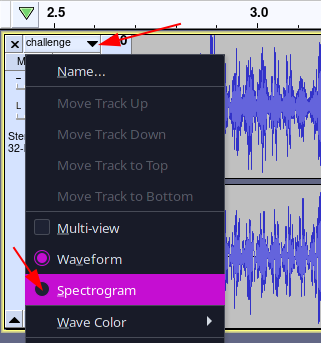
Une fois le spectre affiché, celui-ci se trouver généralement sur une échelle limitée ne dépassant pas 8000 Hz.
Pour afficher le spectre complet (et donc les hautes fréquences), effectuer un clic droit sur l’échelle de fréquence puis Zoom to Fit (ou Zoom Adapté sur la version française).
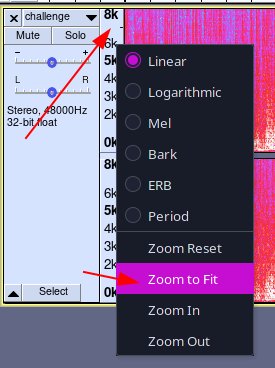
Le spectre est maintenant entièrement affiché.
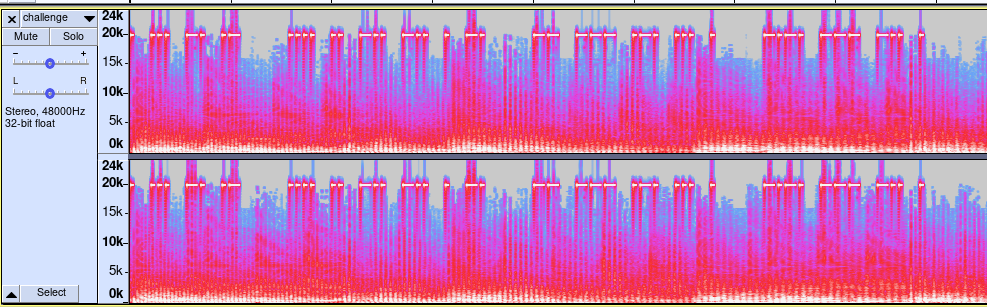
On observe un signal transmis dans les fréquences aiguës à l’aide de signaux courts et longs. Il s’agit enfait du code Morse international, permettant de transmettre du texte à l’aide de séries d’impulsions courtes et longues. Ce même code a permis au prisonnier de guerre Jeremiah Denton de transmettre le mot torture lors d’une interview télévisée à l’aide d’une série de clignements des yeux. Ce message caché a notamment permis de passer outre la censure vietnamienne afin de confirmer pour la première fois l’utilisation de la torture sur les prisonniers américains.
. ... -. .-
.... .. -.. -.. . -.
-- --- .-. ... .
-.-. --- -.. .
Une fois décodé, le code morse devient :
ESNA HIDDEN MORSE CODE
FLAG : ESNA{HIDDEN MORSE CODE}
Music please - Flag 2
Toujours sur le même fichier challenge.wav se trouvait un deuxième message caché.
La musique contenue dans le fichier semble être coupée juste avant le drop de la composition originale (comme l’indique sa durée totale de 31 secondes lors de son ouverture dans un lecteur classique).
La taille du fichier semble par ailleurs anormalement haute (un peu plus de 90 Megaoctets), ce qui correspond généralement à un fichier avec une forte qualité sur plusieurs minutes.
Le fichier aurait donc pu être correctement altéré afin d’en limiter sa lecture.
Afin de réparer le fichier wav, il faut d’abord se renseigner sur son format de fichier :
[Bloc de déclaration d'un fichier au format WAVE]
FileTypeBlocID (4 octets) : Constante « RIFF » (0x52,0x49,0x46,0x46)
FileSize (4 octets) : Taille du fichier moins 8 octets
FileFormatID (4 octets) : Format = « WAVE » (0x57,0x41,0x56,0x45)
[Bloc décrivant le format audio]
FormatBlocID (4 octets) : Identifiant « fmt␣ » (0x66,0x6D, 0x74,0x20)
BlocSize (4 octets) : Nombre d'octets du bloc - 16 (0x10)
AudioFormat (2 octets) : Format du stockage dans le fichier (1: PCM entier, 3: PCM flottant, 65534: WAVE_FORMAT_EXTENSIBLE)
NbrCanaux (2 octets) : Nombre de canaux (de 1 à 6, cf. ci-dessous)
Frequence (4 octets) : Fréquence d'échantillonnage (en hertz) [Valeurs standardisées : 11 025, 22 050, 44 100 et éventuellement 48 000 et 96 000]
BytePerSec (4 octets) : Nombre d'octets à lire par seconde (c.-à-d., Frequence * BytePerBloc).
BytePerBloc (2 octets) : Nombre d'octets par bloc d'échantillonnage (c.-à-d., tous canaux confondus : NbrCanaux * BitsPerSample/8).
BitsPerSample (2 octets) : Nombre de bits utilisés pour le codage de chaque échantillon (8, 16, 24)
[Bloc des données]
DataBlocID (4 octets) : Constante « data » (0x64,0x61,0x74,0x61)
DataSize (4 octets) : Nombre d'octets des données (c.-à-d. "Data[]", c.-à-d. taille_du_fichier - taille_de_l'entête (qui fait 44 octets normalement).
DATAS[] : [Octets du Sample 1 du Canal 1] [Octets du Sample 1 du Canal 2] [Octets du Sample 2 du Canal 1] [Octets du Sample 2 du Canal 2]
* Les Canaux :
1 pour mono,
2 pour stéréo
3 pour gauche, droit et centre
4 pour face gauche, face droit, arrière gauche, arrière droit
5 pour gauche, centre, droit, surround (ambiant)
6 pour centre gauche, gauche, centre, centre droit, droit, surround (ambiant)
NOTES IMPORTANTES : Les octets des mots sont stockés sous la forme Petit-boutiste (c.-à-d., en "little endian")
[87654321][16..9][24..17] [8..1][16..9][24..17] [...
Parmi l’ensemble des blocs décrivant le fichier, le bloc DataSize retient notre attention.
En effet, celui-ci permet de spécifier le nombre de blocs de données audio du fichier.
Si celui-ci a été volontairement décrémenté, alors une partie du fichier ne sera pas lue par les lecteurs.
Le bloc DataSize est facilement identifiable puisqu’il s’agit des 4 octets suivants la constante data.
Nous pouvons dès à présent éditer notre fichier wav dans un éditeur hexadécimal comme hexedit ou encore l’éditeur hexadécimal en ligne HexEd.it.
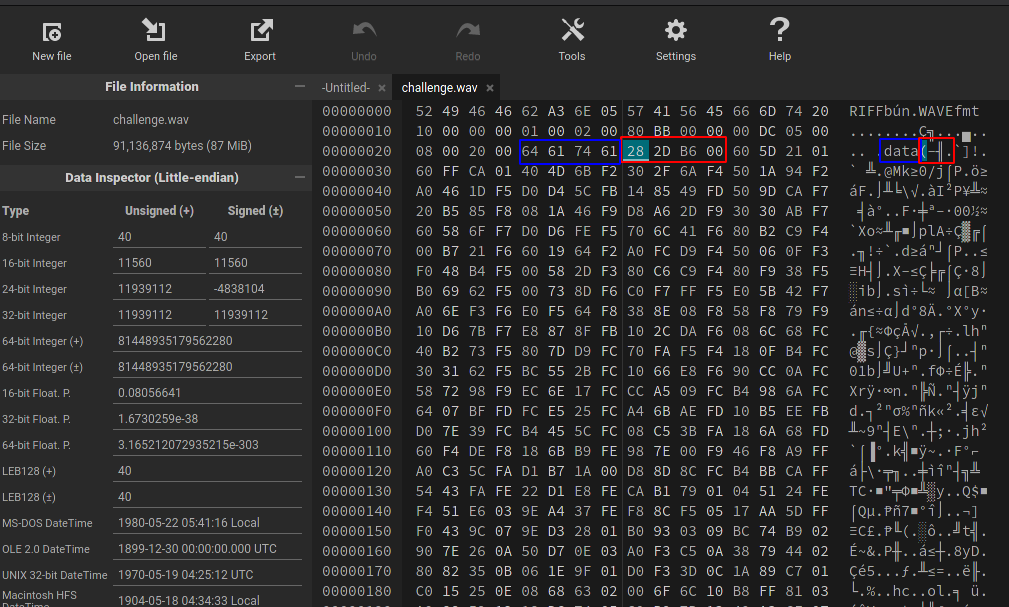
Le contenu du bloc DataSize est donc de 28 2D B6 00.
On remarque que la taille est codée dans l’orientation petit-boutiste (little endian), avec les octets de poids fort vers la fin.
Nous avons donc 0x00B62D28 blocs (11939112).
Nous allons incrémenter cette valeur à 0xFFB62D28 blocs (4290129192), soit la valeur 28 2D B6 FF.
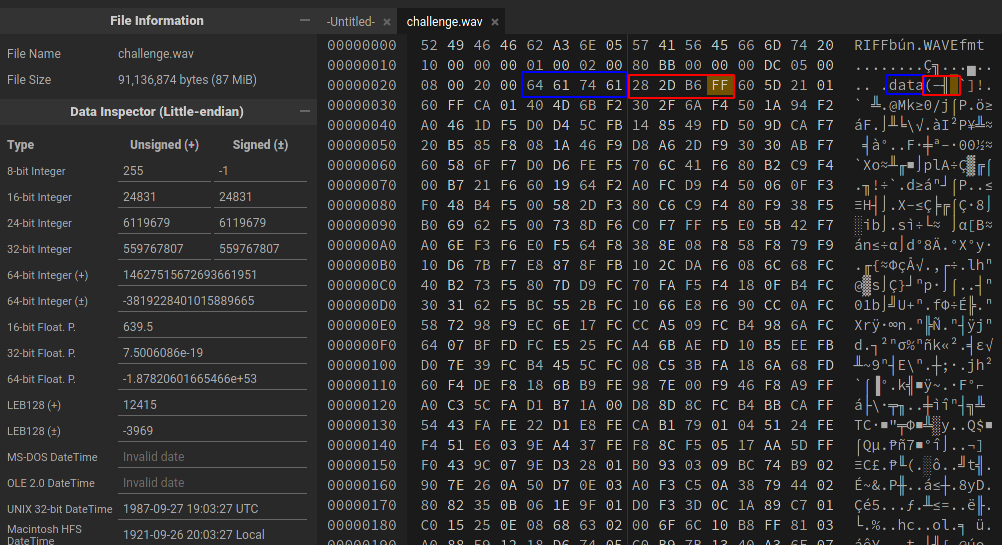
Il suffit ensuite de sauvegarder le fichier et l’ouvrir de nouveau. On observe maintenant que le fichier a une durée de 3:57.

La fin de la musique se termine par une voix avec le message suivant :
Bravo, the flag is in uppercase : ESNA{IMANU_MEMENTO}.
I hope you enjoyed it. If you misspelled the flag, you can verify with the music name.
Flag : ESNA{IMANU_MEMENTO}
Stats - MSE
Pour ce challenge, un fichier cover_image.png et stego_image.png étaient fournis, avec l’énoncé suivant :
Calculer la valeur MSE pour le couple d'image suivant, tronqué 10 chiffres après la virgule.
Format de flag ESNA{XX.XXXXXXXXXX}.
En ayant suivi le cours, ou en recherchant rapidement sur un moteur de recherche, on tombe sur la page Wikipédia de l’Erreur quadratique moyenne (“Mean Squared Error” en anglais). Cette mesure est généralement associée au PSNR, abordé dans le challenge suivant.
L’erreur quadratique moyenne est un estimateur statistique qui, dans le traitement d’images, permet de calculer la différence moyenne des pixels entre deux images. Elle est définie par la formule suivante :
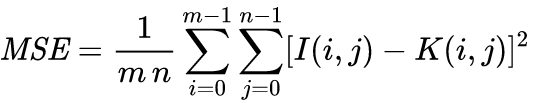
Pour calculer cette valeur, nous utilisons python et la bibliothèque Pillow.
#!/usr/bin/env python3
# pip3 install Pillow
from PIL import Image
img1 = Image.open("cover_image.png")
img2 = Image.open("stego_image.png")
I = list(img1.getdata())
K = list(img2.getdata())
# MSE
s = []
for p in range(len(I)): # p remplace le couple (i,j)
s.append((I[p]-K[p])**2) # (I(i,j) - K(i,j))²
mse = sum(s) / len(s) # somme * 1/(m*n)
print(f"MSE: {mse}")
Nous avons en sortie : MSE: 0.49977941176470586.
Flag : ESNA{0.4997794117}
Stats - PSNR
L’énoncé de ce challenge reprenait les deux mêmes images que le challenge précédent en demandant cette fois-ci la valeur PSNR des deux images. Le PSNR (Peak signal-to-noise ratio), est une mesure de la distorsion qui se calcule directement à partir de l’erreur moyenne quadratique (c.à.d. la valeur MSE calculée dans le précédent challenge). Le PSNR est défini de la façon suivante :
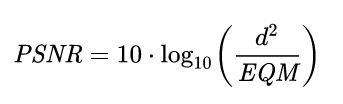
Pour résoudre le challenge, il suffit de reprendre notre script et ajouter le calcul de la formule.
On notera l’import de la fonction log10 de la bibliothèque native math :
#!/usr/bin/env python3
# pip3 install Pillow
from PIL import Image
from math import log10
img1 = Image.open("cover_image.png")
img2 = Image.open("stego_image.png")
I = list(img1.getdata())
K = list(img2.getdata())
# MSE
s = []
for p in range(len(I)): # p remplace le couple (i,j)
s.append((I[p]-K[p])**2) # (I(i,j) - K(i,j))²
mse = sum(s) / len(s) # somme * 1/(m*n)
# PSNR
psnr = 10*log10((255**2)/mse)
print(f"PSNR: {psnr}")
Nous avons en sortie : PSNR: 51.14301999315866.
Flag : ESNA{51.1430199931}
Purple
Le challenge propose un fichier challenge.bmp. La commande exiftool nous donne plus d’indication sur le format de fichier :
$ exiftool challenge.bmp
ExifTool Version Number : 12.14
File Name : challenge.bmp
Directory : .
File Size : 5.3 MiB
File Modification Date/Time : 2021:03:22 12:18:13+01:00
File Access Date/Time : 2021:03:22 12:18:27+01:00
File Inode Change Date/Time : 2021:03:22 12:18:26+01:00
File Permissions : rw-r--r--
File Type : BMP
File Type Extension : bmp
MIME Type : image/bmp
BMP Version : Windows V5
Image Width : 1440
Image Height : 960
Planes : 1
Bit Depth : 32
Compression : Bitfields
Image Length : 5529600
Pixels Per Meter X : 3780
Pixels Per Meter Y : 3780
Num Colors : Use BitDepth
Num Important Colors : All
Red Mask : 0xf8000000
Green Mask : 0x07e00000
Blue Mask : 0x001f0000
Alpha Mask : 0x00000000
Color Space : sRGB
Rendering Intent : Proof (LCS_GM_GRAPHICS)
Image Size : 1440x960
Megapixels : 1.4
Nous avons donc une image bitmap avec les masques suivants :
- Red Mask : 0xf8000000
- Green Mask : 0x07e00000
- Blue Mask : 0x001f0000
En cherchant ces adresses sur internet, on se rend compte que l’image est sauvegardée avec le mode RGB565 (aussi appelé R5G6B5).
Ces chiffres correspondent au nombre de bits alloués par canal (soit un total de 16 bits).
Une recherche R5G6B5 BMP steganography sur internet nous mène à l’article “BMP PCM polyglot”.
Note : le site était également identifiable avec la recherche “BMP 16 bits polyglot”.
L’article nous explique alors qu’il est possible de créer un fichier qui soit à la fois une image BMP valide mais également un son au format raw (PCM). Pour cela, les deux fichiers sources doivent être encodés sur 16 bits (le fichier wav ainsi que le fichier bitmap) afin de générer un BMP codé sur 32 bits. L’article explique que le regroupement des fichiers vient étendre le spectre audio et placer le contenu des pixels dans le spectre inaudible. La définition du masque R5G6B5 permet alors d’indiquer la position des données d’images dans le fichier.
Afin de lire l’image, l’article suggère l’utilisation d’aplay ou audacity.
Pour ce dernier, il suffit lancer l’outil et cliquer sur Fichier > Importer > Données brutes (Raw)... et sélectionner l’image.
Précisez ensuite un encodage Signed 32 bits PCM, un ordre Petit boutiste, les canaux en Stereo avec un échantillonnage à 44100 Hz :
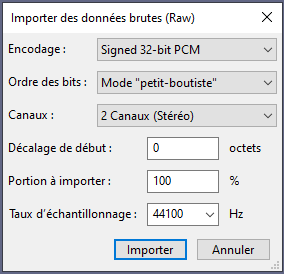
Une fois notre fichier chargé dans audacity, il est possible d’entendre une voix humaine accélérée.
Pour la ralentir, sélectionnen l’audio (CTRL+A) puiss cliquez sur Effets > “Ralentir” et appliquez un ratio de 0,250.

En cliquant sur le bouton play, on entend le message suivant :
GG well play, the flag is in uppercase :
ESNA{LITTLEPOLY}
Flag : ESNA{LITTLEPOLY}
LSB Factory
Ce challenge propose un site web avec un formulaire d’upload et un timer de quelques secondes. Le site web en question nous demande d’encoder un message défini sur une image à l’aide de la technique LSB :
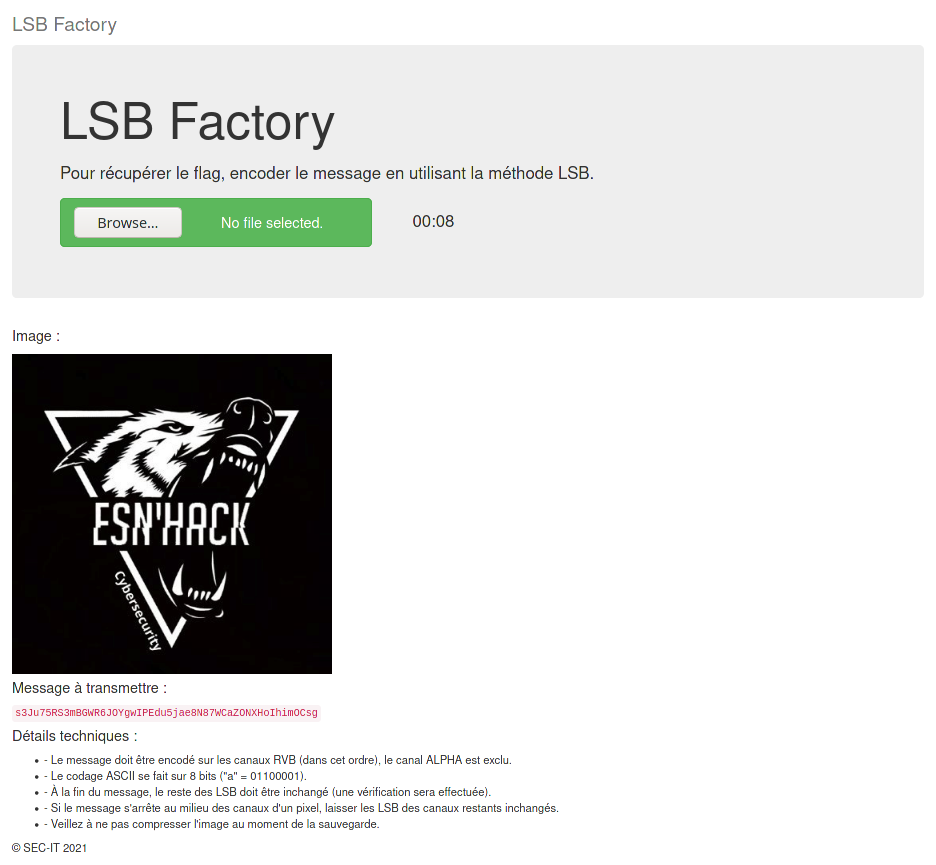
La technique du LSB ayant été abordé pendant le cours précédant le TP, nous invitons le lecteur à se renseigner sur cette méthode pour comprendre la suite de la correction. Afin de résoudre ce challenge, nous allons développer un script python en utilisant la bibliothèque requests pour les requêtes web et pillow pour la gestion de l’image. Un début de script était également fourni en indice, où seule la manipulation des LSB était nécessaire (seules les lignes 33 à 50 étaient manquantes). Voici le script final :
#!/usr/bin/env python3
# pip3 install requests
# pip3 install Pillow
import base64
import io
import requests
from PIL import Image
HOST = "http://51.75.16.174:8000/"
# On créé une session de navigateur
s = requests.session()
# On requète l'index pour avoir le challenge
r = s.get(HOST).text
message = r.split("<code>")[1].split("</code>")[0] # Message attendu
base64_image = r.split('<img src="')[1].split('"/>')[0].replace("data:image/png;base64,","")
cover_image = Image.open(io.BytesIO(base64.b64decode(base64_image))) # Image
cover_image.save("cover_image.png") # On enregistre une copie local du fichier
pxs = list(cover_image.getdata()) # On récupèré la liste de pixels [(255,255,255), (255,255,255), ...]
w,h = cover_image.size # On récupère la taille de l'image
print(f"Taille de l'image : {w}x{h}")
print(f"Message : {message}")
# TODO : Modifier la liste de pixels avec les bons LSB
# On converti le message en binaire
message_bin = ''.join([bin(ord(x))[2:].zfill(8) for x in message])
# On génère la nouvelle image
newpxs = []
x = 0
for i in range(h*w):
r,g,b = pxs[i]
if x < len(message_bin):
r = r - r%2 + int(message_bin[x])
x +=1
if x < len(message_bin):
g = g - g%2 + int(message_bin[x])
x +=1
if x < len(message_bin):
b = b - b%2 + int(message_bin[x])
x +=1
newpxs.append((r,g,b))
stego_image = Image.new(cover_image.mode,cover_image.size)
stego_image.putdata(newpxs)
stego_image.save("stego_image.png") # On enregistre une copie local du fichier
# On envoi la nouvelle image sur le serveur
r = s.post(HOST+"/upload", files={'image': open('stego_image.png','rb')}).text
print(r) # On affiche la réponse du serveur web
De manière plus détaillée :
- Ligne 17 : Première requête web afin de générer le message secret et l’image de support
- Ligne 19 : Récupération du message secret dans une variable
- Ligne 21-22 : Récupération de l’image au format PIL.Image
- Ligne 25 : Conversion de l’image en liste de pixels
- Ligne 34 : Conversion du message secret en binaire
- Ligne 39-50 : Parcours des pixels et modification de la nouvelle liste de pixels en fonction du message secret
- Ligne 39 : Boucle sur l’ensemble des pixels
- Ligne 40 : Récupération du pixel courant et de ses canaux R, G, B
- Ligne 42, 45, 46: On modifie les valeurs des canaux en retirant les LSB et en ajoutant le LSB provenant du message secret
- Ligne 52-54 : Génération de la nouvelle image à partir de la liste de pixels
- Ligne 57 : Envoi de la nouvelle image et récupération de la réponse
- Ligne 58 : Affichage de la réponse
Une fois lancé, le script nous renvoie le flag :
Taille de l'image : 400x400
Message : NhTK372hg6q9AJShcayXxosQhXEOwOERyH3rfJVM60Z29MfvvG
ESNA{I_made_4n_anoying_LSB_Steg0_ch4ll}
Flag : ESNA{I_made_4n_anoying_LSB_Steg0_ch4ll}
Linked List LSB
Ce challenge était le plus difficile de l’ensemble du TP. Pour le résoudre, un papier scientifique est fourni ainsi qu’une image au format PNG. L’article scientifique propose un modèle stéganographique reposant sur la méthode LSB ainsi que sur une répartition des pixels suivant un principe de liste chainée.
Dans cette méthode, un maillon (ou bloc), est représenté par une suite de pixels successifs. La donnée stockée par le bloc (valeur secrète) est codée sur les LSB des 3 premiers pixels. L’adresse du prochain maillon (et donc, le numéro du prochain pixel), est quant à lui stocké sur les LSB restants du bloc.
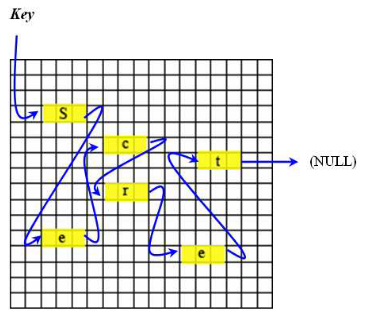
Avec cette technique, la taille d’un bloc dépend de la taille nécessaire pour stocker l’adresse du prochain bloc, et dépend donc indirectement de la taille de l’image. Plus l’image est grande, plus elle a de pixels, plus l’adresse d’un pixel nécessite de bits pour être stockée et plus la taille d’un bloc sera grande.
D’une manière plus précise, la taille nécessaire pour stocker une adresse est définie de la façon suivante :
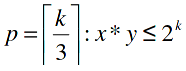
- x*y le nombre de pixels
- k le nombre de bits nécessaires pour stocker une adresse
- k/3 le nombre de pixels nécessaires pour stocker une adresse
La première étape consistait donc à calculer la taille d’une adresse et d’un bloc pour l’image donnée.
Notre image possède une taille de 3840x2160 soit un total de 8294400 pixels. Il faut donc 2^23 bits pour stocker autant d’adresses (ici, k = 23).
En répartissant ce total de 23 bits sur les couches de LSB, on obtient 7 pixels complets ainsi que 2 canaux, soit 8 pixels au total.
La taille d’une adresse est donc de 8 pixels. La taille du bloc est donc de 3 pixels de données + 8 pixels d’adressage soit un total de 11 pixels par bloc.

Une fois la taille d’un bloc calculé, il faut coder une fonction d’extraction pour récupérer à la fois la valeur du secret caché dans le maillon mais également l’adresse du prochain maillon.
Pour notre script, cette fonction prend donc en entrée l’adresse d’un maillon de la liste de pixels data, ajoute le secret du bloc à la variable secret_msg et retourne l’adresse du prochain bloc :
def get_data(addr):
""" Extract byte and return next address addr. """
global secret_msg
s = ""
# First, get data on 3 first pixels
for i in range(8):
c = data[addr+i//3][i%3]
s += str(c%2)
secret_msg += chr(int(s, 2))
# Then we return next address
r = ""
for i in range(nb_px_addr*3):
c = data[addr+3+i//3][i%3]
r += str(c%2)
return int(r, 2)
L’énoncé du challenge nous indiquant l’adresse du premier bloc (Starting pixel : 6075891), une vérification manuelle des résultats de la fonction sur ce premier bloc permet de vérifier le bon fonctionnement de la fonction.
On récupère bien la lettre E et l’adresse du maillon suivant: 2732600.
Le script d’extraction final est le résultat de la fonction get_data et d’une boucle, le tout précédé par le calcul automatique de la taille du maillon:
#!/usr/bin/env python3
# pip3 install Pillow
from PIL import Image
import math
stego_image = Image.open("stego_image.png")
addr = 6075891 # start addr
# First, compute nb of pixels needed for address embeding
w,h = stego_image.size
i, n = 0, 0
while i < (w*h):
n += 1
i = 2**n
nb_px_addr = math.ceil(n/3)
block_size = 3+nb_px_addr
print(f"Pixels needed to embed an address: {nb_px_addr}")
print(f"Pixels per char : {block_size}")
# Decode data
secret_msg = ""
data = list(stego_image.getdata()) # Image data list
size = w*h
def get_data(addr):
""" Extract byte and return next address addr. """
global secret_msg
s = ""
# First, get data on 3 first pixels
for i in range(8):
c = data[addr+i//3][i%3]
s += str(c%2)
secret_msg += chr(int(s, 2))
# Then we return next address
r = ""
for i in range(nb_px_addr*3):
c = data[addr+3+i//3][i%3]
r += str(c%2)
return int(r, 2)
while True:
addr = get_data(addr)
print(secret_msg)
L’exécution du script nous renvoie le flag :
Flag: ESNA{L1nk3d_List_LSB_technique} - https://www.sec-it.fr/ - [end]
À propos
L’article original a été publié sur le blog de mon entreprise https://blog.sec-it.fr/.
Vous pouvez retrouver SEC-IT à l’adresse https://www.sec-it.fr.
Un partie de ce contenu est sous la license MIT / © 2021 SEC-IT.
