Aperi’CTF 2019: Porte Blindée
Challenge details
| Event | Challenge | Category | Points | Solves |
|---|---|---|---|---|
| Aperi’CTF 2019 | Porte Blindée | MISC | 175 | 5 |
Lors d'une mission RED Team, la porte principale de l'entreprise Cybernaise s'est faite attaquée à coup de perceuse.
Les attaquants n'ont pas réussi à rentrer dans les locaux mais la porte est fortement est endommagée et est donc vulnérable.
Afin de renforcer la porte en vue de futures intrusions, il est nécessaire d'établir un blindage sur la zone impactée.
La plaque de blindage étant très couteuse, il est important de minimiser la quantité de matière et donc de minimiser la surface (aire) de cette plaque.
Votre mission est la suivante :
- Déterminer les coordonnées des extrémités de la plaque de blindage de sorte à :
* recouvrir tous les impacts de perceuse
* minimiser la surface (aire) de cette plaque
Attention, vous devez survivre à plusieurs vagues d'intrusions de plus en plus puissante.
Il est important d'indiquer les coordonnées de la plaque de blindage à chaque vague, indépendamment des vagues précédentes.
========================
Details :
- La porte est ici un repère orthonormé où le point [0,0] correspond au centre de la porte
- Chaque trou effectué par la perceuse est modélisé par une coordonnée [x,y]
- La plaque de blindage est rectangulaire
- Vous devez renvoyer une liste de 4 coordonnée sous la forme "(x1,y1);(x2,y2);(x3,y3);(x4,y4)"
- La coordonnées de la plaque doivent être des entiers (valeurs arrondies)
- L'ordre des coordonnées à envoyer n'est pas importante
- L'ordre et les coordonnées d'impacts reçus ne suit pas une logique particulière
- Il y a au minimum 5 impactes par vague
- La notion d'épaisseur de foret n'est pas utile
- La notion d'échelle varie au fur et à mesure des vagues d'attaque, il n'est pas important de s'en soucier.
- Les impacts de perceuse sont compris sur ]-inf,+inf[
- Il n'est pas nécessaire de prendre en compte les impacts des vagues précédentes
- Aumoins 2 syntaxes de réponses sont possibles, comme précisé dans l'exemple.
========================
Exemple de partie :
[Vague 1]
*BANG ! BANG ! BANG*
Impacts: [(-7, 2), (-7, 5), (-6, -2), (-2, 5), (1, 8), (2, -3), (-5, 2), (-5, 5), (-2, -1), (4, 1), (4, 5)]
Installation d'une nouvelle plaque.
>>>[(4, -3), (-7, -3), (-7, 8), (4, 8)]
[Vague 2]
*BANG ! BANG ! BANG*
Impacts: [(-4,2), (-12,4), (-7,-2), (4,5), (6,4), (5,5), (5,-5), (4,8)]
Installation d'une nouvelle plaque.
>>>(6,8);(5,-5);(-13,-3);(-11,10)
[Vague 3]
*BANG ! BANG ! BANG*
Impacts: [(0,3), (2,2), (1,6), (2,1), (3,0), (0,0), (3,3)]
Installation d'une nouvelle plaque.
>>>jkofdjsiodf
[ERREUR] Votre saisie est éronnée !
TL;DR
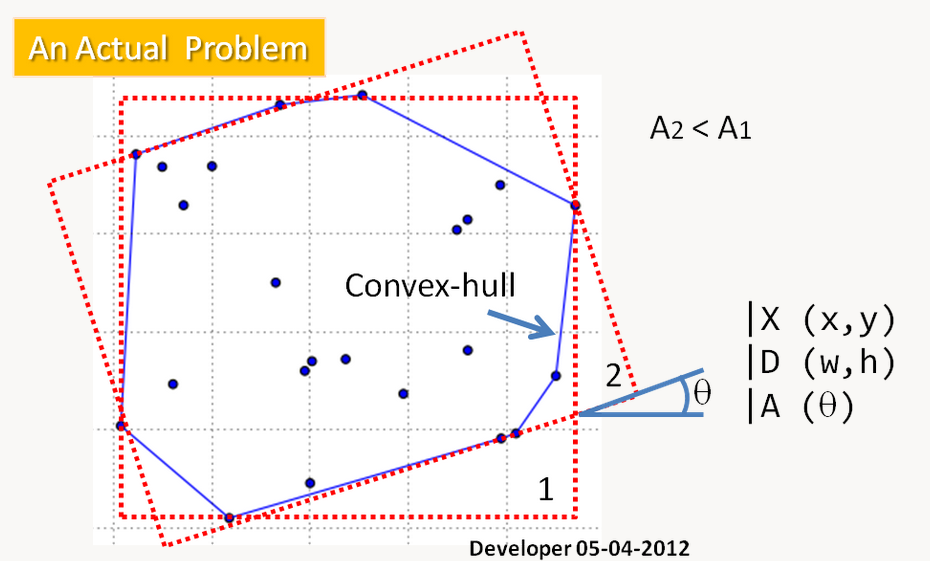
We had a “minimum bounding box” problem also called “minimum bounding rectangle” (MBR).
We had to compute first the convex hull of the given points then compute each bounding box using rotating callipers method (arctan).
Finally we had to look for the best box by comparing each area.
Methodology
Modelizing the problem
After understanding the problem, we looked on google few searches such as: “minimize area cover rectangle”.
We found the following gist topic which explain our problem:
- “How to find the minimum-area-rectangle (MAR) fitted on the given points?”
Convex hull
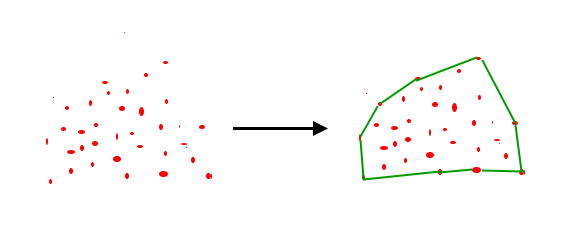
The first point is to compute the “convex hull”. After few search on geeksforgeeks.com, I finally found the algorithm I looked for:
I translated it in python:
def orientation(p, q, r):
"""
Renvoie l'orientation d'un triplet ordonné (p, q, r).
@param p: Point 1
@param q: Point 2
@param r: Point 3
@return: L'orientations du triplet
0 --> p, q and r sont alignés
1 --> Sens horraire
2 --> Sens anti-horraire
"""
val = ((q[1] - p[1]) * (r[0] - q[0])) - \
((q[0] - p[0]) * (r[1] - q[1]))
if (val == 0):
return 0 # Allignés
return 1 if (val > 0) else 2 # Sens horraire / anti-horraire
def convexHull(pts):
"""
Calcul la liste de points composant le "convex hull"
(polygone de taille minimum comprenant tous les points).
@param pts: liste de points d'entrée
@return: list de points composant le convex hull.
"""
hull = []
n = len(pts)
if (n < 3): # 3 points minimums
return None
l = 0
for i in range(1, n): # Recherche du points le plus à gauche
if pts[i][0] < pts[l][0]:
l = i
p = None
while (p != l): # tant qu'on revient pas au début
if p is None: # fix le premier point
p = l
hull.append(pts[p]) # On ajoute le point au convex hull
q = (p+1)%n # On cherche q, point suivant le + antihorraire
for i in range(n):
if (orientation(pts[p], pts[i], pts[q]) == 2):
q = i
p = q
return hull
Minimum Bounding Box
After few search for rotating callipers python implementation, I finally found this one which I decided to modify for our given problem.
You can notice that the algorithm use numpy transposition which is quite similar.
import numpy as np
def minBoundingRect(convex_hull):
"""
Utilise numpy pour convertir un convex hull vers un minimum bounding rectangle
On utilise ici la méthode dite de "rottating callipers".
On cherche à minimiser ou maximiser (@mini) une @condition qui peut soit être
une aire ("area"), soit une largeur ("width")
Inspiration: https://gist.github.com/kchr/77a0ee945e581df7ed25
"""
# Calcule des distances (x2-x1,y2-y1)
dist = np.zeros((len(convex_hull)-1,2))
for i in range(len(dist)):
dist_x = convex_hull[i+1,0] - convex_hull[i,0]
dist_y = convex_hull[i+1,1] - convex_hull[i,1]
dist[i] = [dist_x,dist_y]
angles = np.zeros((len(dist))) # On calcule les angles atan2(y/x)
for i in range(len(angles)):
angles[i] = math.atan2(dist[i,1], dist[i,0])
for i in range(len(angles)): # cast positif
angles[i] = abs(angles[i] % (math.pi/2))
# On retire les doublons
angles = np.unique(angles)
# On vérifie chaque "box" pour optimiser le critère choisi
calc_box = (0, float("inf"), 0, 0, 0, 0, 0, 0) # rot_angle, aire, largeur, hauteur, min_x, max_x, min_y, max_y
for i in range(len(angles)):
# On créer une matrice de rotation pour le convex_hull
# R = [cos(theta), cos(theta-PI/2), cos(theta+PI/2), cos(theta)]
R = np.array([ [ math.cos(angles[i]), math.cos(angles[i]-(math.pi/2)) ], [ math.cos(angles[i]+(math.pi/2)), math.cos(angles[i]) ] ])
# On transpose le convex_hull
rot_points = np.dot(R, np.transpose(convex_hull))
# On récupère les angles de notre rectangle
min_x = np.nanmin(rot_points[0], axis=0)
max_x = np.nanmax(rot_points[0], axis=0)
min_y = np.nanmin(rot_points[1], axis=0)
max_y = np.nanmax(rot_points[1], axis=0)
# On calcule la hauteur,largeur et l'air du rectangle
width = max_x - min_x
height = max_y - min_y
area = width*height
# On optimise
if (area < calc_box[1] or i == 0):
calc_box = ( angles[i], area, width, height, min_x, max_x, min_y, max_y )
# On récupère les angles non transposés
min_x = calc_box[4]
max_x = calc_box[5]
min_y = calc_box[6]
max_y = calc_box[7]
# On recalcule la matrice de rotation
angle = calc_box[0]
R = np.array([[math.cos(angle), math.cos(angle-(math.pi/2))], [math.cos(angle+(math.pi/2)), math.cos(angle)]])
# On retranspose pour avoir les vrais points
points = np.zeros( (4,2) ) # empty 2 column array
points[0] = np.dot([ max_x, min_y ], R)
points[1] = np.dot([ min_x, min_y ], R)
points[2] = np.dot([ min_x, max_y ], R)
points[3] = np.dot([ max_x, max_y ], R)
return (calc_box[1], calc_box[2], calc_box[3], points) # area, width, height, points
Final
Last part is to chain each functions and connect to TCP socket. As usual I decided to use pwntool for this. You can also notice int() and round() as mentionned in the topic.
Final script:
#!/usr/bin/env python3
# -*- coding:utf-8 -*-
import math
import numpy as np
from pwn import *
def orientation(p, q, r):
"""
Renvoie l'orientation d'un triplet ordonné (p, q, r).
@param p: Point 1
@param q: Point 2
@param r: Point 3
@return: L'orientations du triplet
0 --> p, q and r sont alignés
1 --> Sens horraire
2 --> Sens anti-horraire
"""
val = ((q[1] - p[1]) * (r[0] - q[0])) - \
((q[0] - p[0]) * (r[1] - q[1]))
if (val == 0):
return 0 # Allignés
return 1 if (val > 0) else 2 # Sens horraire / anti-horraire
def convexHull(pts):
"""
Calcul la liste de points composant le "convex hull"
(polygone de taille minimum comprenant tous les points).
@param pts: liste de points d'entrée
@return: list de points composant le convex hull.
"""
hull = []
n = len(pts)
if (n < 3): # 3 points minimums
return None
l = 0
for i in range(1, n): # Recherche du points le plus à gauche
if pts[i][0] < pts[l][0]:
l = i
p = None
while (p != l): # tant qu'on revient pas au début
if p is None: # fix le premier point
p = l
hull.append(pts[p]) # On ajoute le point au convex hull
q = (p+1)%n # On cherche q, point suivant le + antihorraire
for i in range(n):
if (orientation(pts[p], pts[i], pts[q]) == 2):
q = i
p = q
return hull
def minBoundingRect(convex_hull):
"""
Utilise numpy pour convertir un convex hull vers un minimum bounding rectangle
On utilise ici la méthode dite de "rottating callipers".
On cherche à minimiser ou maximiser (@mini) une @condition qui peut soit être
une aire ("area"), soit une largeur ("width")
Inspiration: https://gist.github.com/kchr/77a0ee945e581df7ed25
"""
# Calcule des distances (x2-x1,y2-y1)
dist = np.zeros((len(convex_hull)-1,2))
for i in range(len(dist)):
dist_x = convex_hull[i+1,0] - convex_hull[i,0]
dist_y = convex_hull[i+1,1] - convex_hull[i,1]
dist[i] = [dist_x,dist_y]
angles = np.zeros((len(dist))) # On calcule les angles atan2(y/x)
for i in range(len(angles)):
angles[i] = math.atan2(dist[i,1], dist[i,0])
for i in range(len(angles)): # cast positif
angles[i] = abs(angles[i] % (math.pi/2))
# On retire les doublons
angles = np.unique(angles)
# On vérifie chaque "box" pour optimiser le critère choisi
calc_box = (0, float("inf"), 0, 0, 0, 0, 0, 0) # rot_angle, aire, largeur, hauteur, min_x, max_x, min_y, max_y
for i in range(len(angles)):
# On créer une matrice de rotation pour le convex_hull
# R = [cos(theta), cos(theta-PI/2), cos(theta+PI/2), cos(theta)]
R = np.array([ [ math.cos(angles[i]), math.cos(angles[i]-(math.pi/2)) ], [ math.cos(angles[i]+(math.pi/2)), math.cos(angles[i]) ] ])
# On transpose le convex_hull
rot_points = np.dot(R, np.transpose(convex_hull))
# On récupère les angles de notre rectangle
min_x = np.nanmin(rot_points[0], axis=0)
max_x = np.nanmax(rot_points[0], axis=0)
min_y = np.nanmin(rot_points[1], axis=0)
max_y = np.nanmax(rot_points[1], axis=0)
# On calcule la hauteur,largeur et l'air du rectangle
width = max_x - min_x
height = max_y - min_y
area = width*height
# On optimise
if (area < calc_box[1] or i == 0):
calc_box = ( angles[i], area, width, height, min_x, max_x, min_y, max_y )
# On récupère les angles non transposés
min_x = calc_box[4]
max_x = calc_box[5]
min_y = calc_box[6]
max_y = calc_box[7]
# On recalcule la matrice de rotation
angle = calc_box[0]
R = np.array([ [ math.cos(angle), math.cos(angle-(math.pi/2)) ], [ math.cos(angle+(math.pi/2)), math.cos(angle) ] ])
# On retranspose pour avoir les vrais points
points = np.zeros( (4,2) ) # empty 2 column array
points[0] = np.dot( [ max_x, min_y ], R )
points[1] = np.dot( [ min_x, min_y ], R )
points[2] = np.dot( [ min_x, max_y ], R )
points[3] = np.dot( [ max_x, max_y ], R )
return (calc_box[1], calc_box[2], calc_box[3], points) # area, width, height, points
LHOST = 'porte.aperictf.fr'
LPORT = 4444
r = remote(LHOST, LPORT)
for i in range(100):
rec = r.recvuntil(">>>")
entree = eval(rec.split("Impacts: ")[1].split("\r\n")[0])
ch = convexHull(entree) # Convex Hull
mbr = minBoundingRect(np.array(ch)) # MBR
mbr = str([(int(round(x[0])),int(round(x[1]))) for x in mbr[-1]])[1:-1] # On cast en tuple
print(rec)
print(entree)
print(mbr)
r.sendline(mbr)
r.interactive()
Flag
APRK{.I.l0v3.G30M3TRY.}
