BreizhCTF 2023 - Smoll Grid

Challenge details

Event	Challenge	Category	Points	Solves
BreizhCTF 2023	Smoll Grid	Programmation	???	???

Vous commencez dans le coin supérieur gauche d’une grille 6 × 6 et votre objectif est de vous déplacer vers le coin inférieur droit. Vous ne pouvez vous déplacer que dans deux directions : vers la droite ou vers le bas. Les mouvements en diagonale et en arrière sont interdits.

Combien y a-t-il de façons différentes d’aller du début à la fin ? (3 exemples de chemins sont proposés dans le fichier associé).

Le Flag est sous la forme BZHCTF{N} où N est un entier positif non nul.

Auteur: Zeecka

TL;DR

Une approche combinatoire ou utilisant le triangle de Pascal permet de trouver le résultat 252.

Méthodologie

Un article détaillé de Geeks for Geeks expose le problème.

L’approche du triangle de Pascal est la suivante :

Si on connaît le nombre de chemins possibles pour atteindre la case de gauche et une case du haut d’une case donnée, alors, le nombre de chemins pour arriver à la case donnée, sera la somme des deux.

Comme le montre la figure, nous pouvons atteindre la case de gauche de A manières différentes et atteindre les blocs supérieurs de B manières différentes, donc la réponse totale de notre nouvelle case sera A+B. La répétition de ce principe permet de réaliser le schéma suivant :

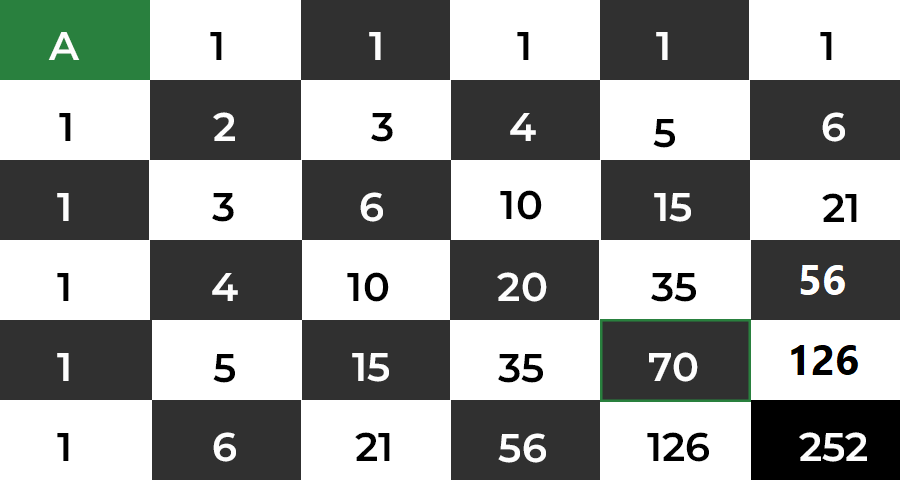
Le nombre de possibilités est donc de 252.

Flag

BZHCTF{252}

Auteur: Zeecka